Thermodynamique : les lois

L’invention de la machine à vapeur par Thomas Newcomen, puis son perfectionnement par James Watt, survenus à la fin du 18^ème siècle, ont largement  précédé la science qui leur est consacrée (Lire : Une brève histoire de l’énergie). De fait, la thermodynamique n’a atteint sa formulation classique que dans la deuxième moitié du 19^ème.  À mi-distance entre ces deux dates, Sadi Carnot a posé les fondations de cette science, dans son unique livre Réflexions sur la puissance motrice du feu publié en 1824[1].  Emporté jeune par la maladie, il n’a pas publié d’autre ouvrage sur une recherche entreprise simultanément avec son métier militaire. Emile Clapeyron a  découvert l’ouvrage et l’a sorti de l’oubli dans un article publié en 1832 où il reformule mathématiquement les démonstrations de Carnot dont il dit : « L’idée qui sert de base à ses recherches me paraît féconde et incontestable, ses démonstrations reposent sur l’absurdité qu’il y aurait à admettre de créer de toutes pièces de la force motrice ou de la chaleur »[2].

En adoptant l’idée de base de Carnot comme fil directeur, complétée par les éclairages ou corrections amenées par ses successeurs, en particulier William Thomson (Lord Kelvin), la thermodynamique peut être présentée avec un minimum de formulations mathématiques.

1. Le phénomène essentiel dans une machine à vapeur

Carnot s’affranchit des détails techniques d’une machine à vapeur pour aller à l’essentiel. L’eau est l’agent de la production de puissance motrice : elle suit un cycle de transformations grâce à la mise en circulation par une pompe. Sous haute pression, elle entre dans un faisceau de tubes chauffé par la combustion dans la chaudière où elle est vaporisée. Ensuite la vapeur se détend dans un moteur à piston du temps de Carnot, et dans une turbine aujourd’hui, où elle développe la puissance motrice. Ensuite la vapeur passe dans un autre faisceau de tubes, refroidi de l’extérieur ; elle y est condensée pour retrouver l’état liquide initial avant d’être pompée à nouveau vers l’entrée de la chaudière et recommencer un cycle. « La production de puissance motrice est donc due dans les machines à vapeur non à une consommation réelle du calorique mais à son transport d’un corps chaud à un corps froid. (…) D’après ce principe, il ne suffit pas, pour donner naissance à la puissance motrice, de produire de la chaleur : il faut encore se procurer du froid. »[3]. L’invention par Watt du condenseur refroidi par l’eau d’une rivière ou l’air ambiant, relevait de cette constatation et avait apporté une amélioration notable.

Suivant Carnot, la vapeur d’eau n’est pas le seul corps capable de réaliser cette puissance motrice qui peut être réalisée par n’importe quel corps capable de dilatation et de contraction avec l’alternance de chaud et de froid : solides et liquides (à quelques rares exceptions), gaz  ou vapeurs. Les vapeurs ou les gaz étant les plus dilatables (ou compressibles), sont employés dans les moteurs thermiques. On utilise en particulier l’air chauffé par combustion et c’est lui qui sera retenu dans la suite. Une masse de gaz se dilate quand elle est chauffée et se contracte quand elle est refroidie. Mais, inversement, elle s’échauffe quand elle est comprimée et se refroidit quand elle est dilatée.

2. La production de puissance motrice à partir de la chaleur

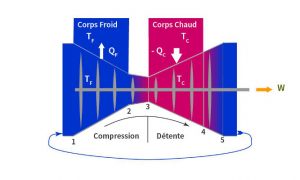
En s’autorisant un anachronisme, la démonstration de Carnot peut être suivie à l’aide d’un turbocompresseur, inventé plus d’un siècle plus tard. Ce moteur est utilisé pour la propulsion des avions ou la production électrique dans les centrales à gaz. Il rend la démonstration plus aisée que le moteur à piston utilisé par Carnot sans trahir sa démonstration qui a valeur universelle. Tout comme Carnot l’a fait avec le moteur à piston, c’est une version idéalisée du turbocompresseur, représentée par la Figure 1, qui servira à la démonstration.

L’air qui entre, à pression et température ambiante, traverse en premier le compresseur : son volume spécifique diminue et sa pression monte, ce qui élève sa température. Pour maintenir l’air à la valeur T_F, il faut évacuer la chaleur produite par la compression à mesure qu’elle se forme, ce qui est fait par contact thermique parfait avec un corps maintenu à la température T_F. C’est l’étape qui va de 1 à 2, celle de la compression isotherme, qui se produit à température constante. De 2 à 3, l’air poursuit sa compression en étant thermiquement isolé ; sa température s’élève sous l’effet de la compression adiabatique qui se fait sans perte de chaleur. La compression s’arrête en 3 lorsque la température de l’air atteint la température T_C .

L’air passe alors dans la turbine et se dilate. De 3 à 4, il est en contact thermique parfait avec le corps chaud à température T_C  qui lui fournit continument la chaleur nécessaire pour enrayer la chute de température accompagnant la dilatation du gaz. La dilatation est isotherme. Avant d’atteindre la pression ambiante, l’air est isolé thermiquement et la fin de la détente adiabatique qui se fait sans gain de chaleur, ramène l’air aux conditions initiales de pression ambiante et température T_F. Revenu aux conditions initiales, l’air peut recommencer un cycle.

La  détente du gaz produit du travail, la compression en consomme. L’élasticité du gaz s’accroissant avec la température et la détente ayant lieu à la température chaude du cycle, elle produit  plus de travail que la compression n’en consomme. Aussi le bilan du moteur est la production d’un travail W compté avec un signe positif car il est un apport pour l’extérieur. Le moteur absorbe la quantité de chaleur -Q_C , négative, car elle est dépensée par le corps chaud extérieur.  Il relâche une quantité de chaleur Q_F, positive, car elle est un apport au corps froid extérieur.

3. La réversibilité : condition pour produire l’action maximale

Carnot énonce ce principe : « Partout où il existe une différence de température, il peut y avoir une production de puissance motrice »[4]. Il s’en suit que « tout rétablissement de calorique [i.e. égalisation des températures par le passage de la chaleur du chaud au froid] sans production de puissance motrice est une perte ». Aussi, « le maximum de puissance motrice est obtenu à la condition qu’il ne se fasse dans les corps employés à la puissance motrice, aucun changement de température qui ne soit dû à un changement de volume. »[5].

La machine décrite remplit bien ces conditions. En effet, il n’y a aucun passage de chaleur entre les corps chaud et froid en dehors de l’action de l’air dans le moteur. Au moment du contact de l’air avec les corps chaud et froid, l’écart de température, nécessaire au passage de la chaleur du chaud vers le froid, peut être réduit à la limite à zéro. La température de l’air ne varie que lors des changements de volume accompagnant la compression (1-2) ou la détente (4-5) qui sont adiabatiques, donc sans fuite de chaleur.

Les machines réelles peuvent juste tendre vers ce fonctionnement sans perte qui représente un cas idéal. Et puisque ce cas idéal est sans perte, le sens de ses transformations peut être inversé à tout moment et produire des effets exactement opposés à ceux du sens direct.

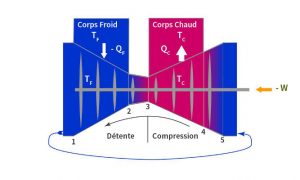
La Figure 2, décrit le cycle inverse obtenu en fournissant à la machine un travail W. L’air entrant subit d’abord une compression adiabatique de 5 à 4 qui échauffe l’air jusqu’à T_C. La compression est poursuivie de 4 à 3 au contact du corps chaud qui évacue la chaleur produite par la compression et maintient l’air à la température T_C. De 3 à 2, la détente adiabatique abaisse la température jusqu’à T_F. Puis de 2 à 1 la détente est poursuivie au contact du corps froid qui compense la perte de chaleur de l’air due à la détente et maintient l’air à la température T_F.  Ainsi, les échanges de chaleur sont inverses du cas direct : le corps chaud reçoit Q_C et le corps froid fournit – Q_F parce qu’un travail –W a été fourni de l’extérieur.

Le bilan net est donc un transport de chaleur de la source froide à la source chaude, contraire au passage spontané du chaud vers le froid. Ceci est possible grâce à la dépense dans la machine d’un travail – W. C’est le fonctionnement d’un réfrigérateur ou d’une pompe à chaleur.

4. Démonstration du maximum d’action par Carnot

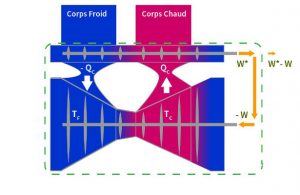
Le maximum de puissance motrice possible a-t-il été atteint pour la quantité de chaleur fournie par le corps chaud avec la machine décrite dans la Figure 1 ? Oui, prouve Carnot grâce au raisonnement par l’absurde suivant. Supposons qu’il existe une machine Z qui produise un travail W* supérieur à W avec la même quantité de chaleur Q_C. On peut utiliser le travail W* pour faire fonctionner la machine réversible dans le sens inverse, comme la pompe à chaleur dans la Figure 2, et associer les deux machines suivant le système décrit dans la Figure 3.

La pompe à chaleur a besoin d’une dépense de travail -W  pour amener la quantité de chaleur Q_C à la source chaude. Ainsi, la pompe à chaleur fournirait à la machine Z la chaleur Q_C qu’elle aurait puisé autrement dans le corps chaud. Ayant supposé que la machine Z fournirait un travail W*  supérieur à W, il resterait un surplus (W* – W) de travail pour l’extérieur. Par ailleurs, la pompe à chaleur soutirerait toute la chaleur que Z rejetterait autrement dans le corps froid (Carnot se trompe ici, mais poursuivons sa démonstration). La pompe à chaleur fournirait au moteur Z le chauffage et le refroidissement qui sont nécessaires à son fonctionnement. Le système constitué du moteur Z et de la pompe à chaleur, isolé du reste du monde extérieur par la frontière verte, fonctionnerait sans transfert de chaleur avec les corps chaud et froid et sans aucun autre apport. Mais il fournirait à l’extérieur le surplus de travail (W* – W) : « ce serait là non seulement le mouvement perpétuel, mais une création indéfinie de force motrice, sans consommation ni de calorique ni de quelque autre agent que ce soit. Une semblable création est tout-à-fait contraire aux idées reçues jusqu’à présent, aux lois de la mécanique et de la saine physique ; elle est inadmissible. »[6].

5. La première loi de la thermodynamique (dite de Joule)

L’erreur de Carnot a consisté à supposer que la quantité de chaleur Q_C est intégralement transportée de la source chaude à la source froide. Bien qu’il ait émis des doutes sur la validité de la théorie de la chaleur de son temps, il a succombé à son erreur. La Figure 3 contient cette erreur, contrairement aux Figures 1 et 2 où les quantités de chaleur échangées avec les corps chaud et froid Q_C et Q_F sont bien distinctes.

Les résultats expérimentaux de James Prescott Joule[7] publiés plus de 20 ans après la publication de Carnot démontrent clairement la nécessité de distinguer Q_C et Q_F et l’erreur qu’on commet en les confondant. Cette expérience utilise un calorimètre (conteneur isolé thermiquement de l’extérieur comme les bouteilles thermos) où on peut déterminer des quantités de chaleur générées par combustion ou autre moyen quand on connait la capacité calorifique interne et qu’on mesure l’élévation de température. Pour son expérience Joule a inclus, dans le calorimètre, le dispositif mécanique suivant : des ailettes, fixées à un axe vertical entraîné par un moteur, brassent le liquide contenu dans le calorimètre. La viscosité du liquide oppose une résistance au mouvement des ailettes et le moteur fournit un travail pour maintenir la vitesse de rotation. La température s’élève dans le calorimètre : de la chaleur est générée avec la résistance du liquide au mouvement du moteur. En répétant l’expérience dans différentes conditions, Joule montre que la quantité de chaleur générée est dans un rapport constant avec le travail fourni pour compenser la résistance. Elle lui est égale si on prend le même système d’unités pour la chaleur et la mécanique, ce que fait le système international d’unités (SI) qui adopte le joule (J) comme unité de travail ou de chaleur.

La première loi de la thermodynamique en résulte et elle peut être énoncée ainsi d’après Thomson[8]: « Prop. I. (Joule) – Quand des quantités égales de travail sont produites par un moyen quelconque à partir de sources purement thermiques, ou sont dissipées en effets purement thermiques, des quantités égales de chaleur sont détruites ou générées ».

6. La deuxième loi de la thermodynamique (dite de Carnot)

Cette première loi permet d’évaluer le transport de chaleur du corps chaud au corps froid, base de la production de puissance motrice suivant Carnot. Au cours de ce transport, une quantité de chaleur est détruite, égale au travail produit. Aussi, dans la Figure 1, le corps froid reçoit la quantité extraite du corps chaud diminuée de la chaleur détruite lors de la production de travail : Q_F = Q_C – W. Dans le fonctionnement inverse de la Figure 2, la quantité de chaleur reçue par le corps chaud Q_C est la quantité de chaleur extraite du corps froid Q_F augmentée de la quantité de chaleur générée par la dissipation du travail W : Q_C = Q_F+ W. Les deux équations sont évidemment  identiques.

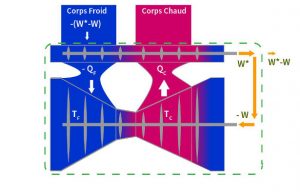
 À présent, on peut reprendre la démonstration de Carnot et voir que, malgré l’erreur glissée dans la démonstration, son résultat est exact. Il faut toutefois énoncer autrement l’impossibilité sur laquelle débouche le raisonnement par l’absurde. C’est ce qu’ont fait deux autres fondateurs de la thermodynamique, William Thomson et Rudolf Clausius, qui disposaient des résultats de Joule et ont donné, vingt ans après Carnot, des démonstrations qui respectent la première loi de la thermodynamique. La Figure 4 accompagne la démonstration de Thomson.

Les deux machines sont associées comme par Carnot. Le moteur Z reçoit de la pompe à chaleur la quantité de chaleur Q_C nécessaire à son fonctionnement. Le moteur produit plus de travail W* que nécessaire pour la pompe à chaleur. Il reste un solde positif de travail W* – W pour l’extérieur. La première loi de la thermodynamique dit que cet excès de travail est accompagné d’une destruction égale de chaleur. Le corps froid devrait compenser cette destruction en apportant de la chaleur, ce qui baisserait localement sa température. Ceci est impossible car contraire à l’axiome[9] énoncé par Thomson : « Il est impossible, par un agencement de matière inanimée, de tirer un effet mécanique d’une quelconque portion de matière en la refroidissant en dessous de la température la plus basse du milieu qui l’entoure »[10]. Sinon,  par exemple, un bateau, pourrait être propulsé par un moteur alimenté sans  autre source d’énergie que l’océan où de la glace serait laissée dans le sillage du bateau.

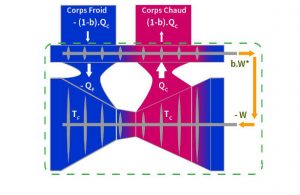
Clausius, utilisant un autre axiome, donne la démonstration illustrée par la Figure 5. Au lieu que le moteur Z fournisse le travail W*, son régime est ralenti de façon à ce qu’il produise W, la quantité de travail juste nécessaire au fonctionnement de la pompe à chaleur. Soit b le rapport de réduction, tel que b.W* = W. Alors l’apport de chaleur b.Qc suffit  au régime réduit du moteur Z et il reste une partie de la chaleur apportée par la pompe à chaleur qui n’est pas utilisée par le moteur. Cette chaleur excédentaire, cédée au corps chaud, vaut : (1–b).Qc. Mais, tout étant égal par ailleurs dans le système, la première loi indique que cette chaleur transmise au corps chaud doit être égalée par une quantité de chaleur égale en provenance du corps froid. Aussi le contour vert contient un dispositif qui, sans apport, transmettrait de la chaleur d’un corps froid à un corps chaud, ce qui est contraire à l’axiome énoncé par Clausius[11] : « Il est impossible, par une machine autonome, sans aucun apport extérieur, de transporter de la chaleur d’un corps à un corps plus chaud. ».

En conclusion, même si « ces deux axiomes sont différents dans leur forme, l’un est la conséquence de l’autre. Le raisonnement suivi dans chaque démonstration est strictement analogue à celui que Carnot a donné à l’origine »[12] .  Dans cette phrase, Thomson synthétise clairement l’identité des vérités auxquelles Clausius et lui sont arrivées avec celle découverte vingt ans plus tôt par Carnot.

Il énonce ainsi la deuxième loi de la thermodynamique : « Prop II (Carnot et Clausius) – Si une machine est telle qu’en inversant son sens de fonctionnement, les actions physiques et mécaniques sont inversées à toutes les étapes de son mouvement, elle produit le maximum d’action mécanique possible à toute machine utilisant une quantité donnée de chaleur, entre les mêmes températures chaude et froide »[13].

L’énoncé de ces deux premières lois, la première découverte par Joule, la deuxième par Carnot, est le fondement de la thermodynamique. Il reste à évaluer le travail qui peut être produit à partir d’une quantité de chaleur donnée (Lire : Thermodynamique : énergie et entropie).