Hors hydraulique, toutes les filières renouvelables ne sont pas à des stades égaux de développement. Certaines machines telles que les hydroliennes ne datent réellement que du 21ème siècle. Il faut donc tout apprendre à leur sujet, en commençant par ce qui les distingue des éoliennes.
Dès la fin du 19ème siècle, quelques scientifiques avaient évoqué l’idée de capter l’énergie mécanique des courants marins, mais ce n’est que depuis la première décennie du 21ème siècle que cette source d’énergie a commencé à être étudiée très sérieusement et que des hydroliennes sont construites. Avant d’examiner les caractéristiques des turbines, les modalités de leur carénage, les limites de leur rendement et les ressources exploitables, la parenté entre hydroliennes et éoliennes doit focaliser l’attention.
1. Hydroliennes versus éoliennes
Le but d’une hydrolienne est de récupérer l’énergie cinétique des courants marins ou fluviaux pour faire tourner le rotor d’une turbine immergée. Il s’agit donc d’une transposition marine du rotor éolien qui récupère l’énergie cinétique du vent (Lire : Énergie éolienne, des gisements aux aérogénérateurs et L’éolien en haute altitude).
1.1. Une filiation évidente
La Figure 2 présente la confrontation éolienne-hydrolienne pour une autre famille de turbines dites à axe de rotation vertical. On les appelle aussi turbines à flux transverse car le courant incident doit arriver perpendiculairement à l’axe de rotation qui peut donc être horizontal. La photo de gauche présente la plus grande éolienne à flux transverse du monde, développée par le laboratoire américain Sandia et installée en Gaspésie (Quebec) au Cap Chat. Elle fait 110 m de haut et développe 4 MW. L’image de droite présente le prototype d’hydrolienne de la Société New Energy Inc. (Calgary, Alberta) de 1,52 m de diamètre. Il a été testé en 2007. Au-delà du facteur d’échelle entre les deux turbines, une différence notable dans leur design apparait : l’éolienne possède une géométrie de pales en forme de parabole alors que l’hydrolienne utilise des pales droites. La forme parabolique provient de la prédominance dans l’air des forces centrifuges sur les forces aérodynamiques s’appliquant sur les pales. Les pales sont calculées en annulant les efforts de flexion le long de leur ligne moyenne.
On obtient ainsi une forme de corde à sauter dite troposkienne. Pour des rotors éoliens de petite taille on peut s’affranchir de la forme troposkienne en renforçant la structure (figure 3, gauche) ; on notera la forme hélicoïdale qui présente quelques avantages (voir plus loin) . Dans l’eau, la forme troposkienne n’est pas utilisée car les forces hydrodynamiques prédominent (Figure 3, droite).
1.2. Un cahier des charges analogue
Lorsqu’il s’agit d’installer un dispositif de taille significative, comme un parc d’hydroliennes ou d’éoliennes, il est nécessaire de prendre en compte des contraintes qu’il est usuel de regrouper en trois catégories : sociétale, environnementale et économique.
La dimension économique est la clé de voute de tout projet industriel. Deux ingrédients majeurs sont nécessaires au développement d’une filière : l’existence d’un marché, et la capacité de produire à un coût compétitif ; ces ingrédients sont toutefois liés. Pour l’éolien, le photovoltaïque et la plupart des énergies renouvelables conduisant à la production d’électricité, le coût de production du kWh reste supérieure à celui des filières traditionnelles telles que le gaz, l’hydraulique ou le nucléaire. En ce sens, le kWh produit n’est pas, pour l’instant, compétitif. Pour cette raison, le développement de l’éolien est favorisé dans la plupart des pays par un tarif incitatif du kWh, garanti sur la durée d’exploitation qui est de 15 ans en France. La technologie des hydroliennes n’est pas assez mature pour que l’on puisse aujourd’hui évaluer son coût avec précision. Comme un grand nombre de technologies sont proposées, il faudra attendre les retours d’expériences pour y voir plus clair. Il est probable que les systèmes se révélant les meilleures sur certains sites (mer ou fleuve, isolé ou non, sujet aux tempêtes ou non) seront moins adaptés sur d’autres.
1.3.Avantages et inconvénients respectifs
Les hydroliennes possèdent essentiellement trois avantages sur les éoliennes : leur discrétion, leur compacité et la prédictibilité de leur production. Cependant, il faut avoir en tête que la ressource hydrolienne est bien moins importante que la ressource éolienne (près de deux ordre de grandeur).
Même si la plus puissance hydrolienne du monde (1,2 MW, double turbine) est montée sur un pieu comme une éolienne off-shore (Figure 4, gauche), de nombreux développeurs proposent aujourd’hui des concepts complètement immergés (Figure 4, centre et droite). Ainsi, la discrétion visuelle est assurée, au moins pour les humains. Pour ce qui est de l’émission sonore d’un parc sous l’eau, elle est évaluée comme équivalente à celle d’un gros navire.
La relation P = 1/2 ρS V3 montre que la puissance d’une turbine est proportionnelle à la masse volumique du milieu r et au cube de la vitesse du courant V (Cp étant le coefficient de puissance et S la section de l’aire balayée par les pales de la turbine).
En prenant 2m/s et 1000kg/m3 pour l’eau et 10m/s et 1.2kg/m3 pour l’air, on montre qu’une même puissance est obtenue dans l’eau avec un rotor de dimension réduite d’un facteur 3 par rapport à l’air. Par exemple, 1 MW obtenu avec un rotor de 50m de diamètre dans l’air est obtenu avec un rotor de 18m dans l’eau. Ceci conduit à des équipements plus légers qui devraient se révéler moins couteux. À titre d’exemple, l’éolienne E-126 (1,2 MW pour 3 750 tonnes) produit 1,9 kW par tonne alors que l’hydrolienne MCT Seagen (1 200 kW pour 390 tonnes) produit 3 kW par tonne et la turbine Hammerfest Ström (300 kW pour 107 tonnes) produit 2,8 kW par tonne. Outre la raison purement hydrodynamique, la compacité d’une hydrolienne vient aussi de ses conditions d’exploitation : une hydrolienne est en effet dimensionnée pour exploiter la vitesse quasi-maximum du courant (les événements exceptionnels comme les crues et les grandes marées ne donnent pas lieu à des vitesses bien plus fortes) ; en comparaison, l’éolienne n’exploite le vent que jusqu’à 90 km/h tandis que sa structure doit résister à des vents de 300km/h.
La prédictibilité de la production d’un hydrolienne vient du fait que les courants de rivières et des marées sont parfaitement connus et possèdent un caractère régulier dont le vent est démuni. Les courants de rivières sont constants à l’échelle de la journée (en dehors des événements de crue) et les courants marémoteurs fluctuent sinusoïdalement sur une période de 12h environ (sur les cotes européennes). La gestion de la production d’électricité est par conséquent facilitée par rapport aux éoliennes, sans pour autant que l’on puisse éluder la question du stockage : pour la rivière, la sécheresse ou la crue sont des événements empêchant la production ; pour les marées, l’étale est aussi une période non productive. À l’inverse, et comme pour toute production d’électricité, la question du stockage, aux périodes creuses, reste pertinente.
2. Turbines fondées sur le principe de la portance hydrodynamique
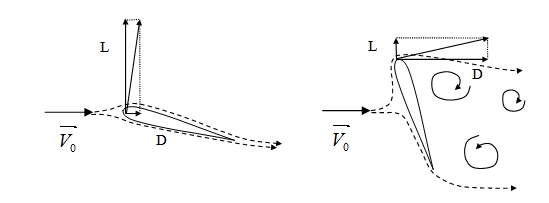
Un profil plongé dans un courant uniforme subit un effort de portance, noté L, dont la composante est perpendiculaire au courant incident et un effort de trainée, noté D, dont la composante est le long du courant. La théorie des fluides à potentiel montre que la portance est un phénomène non visqueux. En revanche, la trainée met en jeu un mécanisme de frottement des filets fluides les uns sur les autres, appelé dissipation. Cette dissipation dégrade, d’une façon irréversible, l’énergie mécanique du fluide (énergie de pression + cinétique + hauteur) en énergie thermique. Cette dernière représente donc une perte. Le rendement d’un rotor, qui rapporte l’énergie mécanique récupérée à l’énergie disponible dans le fluide, sera d’autant meilleur que la dissipation sera faible. En conséquence, on obtient généralement de meilleurs rendements pour des turbines mues par les forces de portance plutôt que pour celles mues par les forces de trainée.
La Figure 5 de gauche, représente un écoulement autour d’une aile placée dans un écoulement à faible incidence. Les filets fluides restent près du profil et créent une dépression au-dessus (extrados) et une dépression en dessous (intrados). Ce champ de pression est à l’origine de la force de portance, bien plus forte que la force de trainée. La figure de droite représente le même profil placé à forte incidence. Les filets fluides ne peuvent suivre le profil, ils décollent. La face amont du profil est en surpression et la face aval en dépression. La force de trainée qui en résulte est dans ce cas bien plus importante que la force de portance. Le sillage tourbillonnaire se développant à l’aval est turbulent et très dissipatif. Un déplacement vertical sur le schéma gauche aura un meilleur rendement qu’un mouvement vers la droite sur le schéma de droite
2.1. Turbines à flux axial
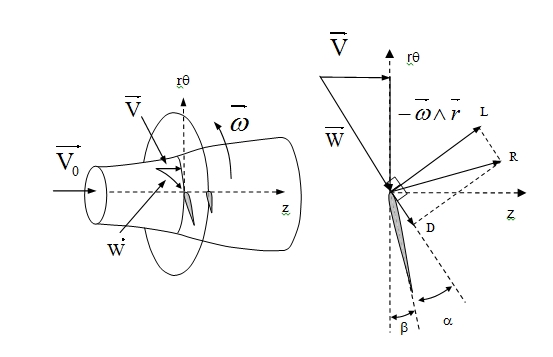
Pour comprendre le principe de fonctionnement de la turbine, il faut représenter les pales en coupe dans un tube de courant contenant les vecteurs[1] vitesse (Figure 6). Ainsi, la pale voit une vitesse relative amont W donnée par :
W⃗ =V⃗ −ω⃗ ∧r⃗
où V est la vitesse axiale moyenne au niveau du rotor (plus faible que celle à l’amont), et r le rayon vecteur joignant l’axe de rotation au point considéré.
R, la résultante des efforts sur la section de pale, se décompose en une portance L et une trainée D. L’angle b est le calage de la section de pale et l’angle a l’incidence de l’écoulement relatif W. La figure montre que le couple obtenu sur l’axe de rotation provient de la projection de la portance sur l’axe q diminué de la projection de la trainée sur ce même axe. Le dimensionnement du rotor consiste à placer la section de pale sous la meilleure incidence pour que la force de trainée soit la plus faible possible comparativement à la force de portance.
2.2. Turbines à flux transverse
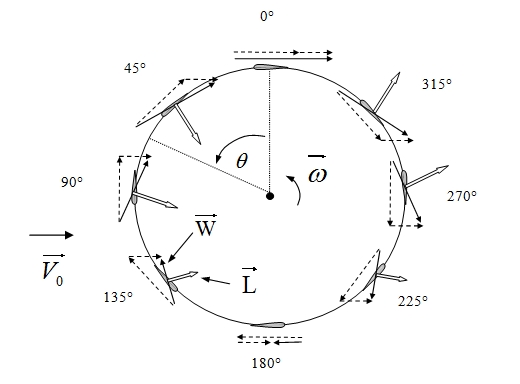 La Figure 7 présente une coupe de turbine à flux transverse par un plan perpendiculaire à l’axe de rotation. (turbines de la Figure 3 b) ou de la Figure 9). L’écoulement est supposé contenu dans ce plan. Le vecteur pointillé horizontal représente la vitesse axiale locale au niveau de la section de pale (inférieure à V0). L’autre vecteur pointillé représente l’opposé de la vitesse de rotation du profil. La somme de ces vecteurs, la flèche en trait plein, représente la vitesse relative W vue par le profil. La différence avec le rotor à flux axiale est que le profil voit un écoulement relatif variable en intensité et en direction au cours de sa rotation. L’écoulement est par conséquent instationnaire dans le repère relatif. Le vecteur plus épais représente l’effort subi par la section de pale. Bien que l’écoulement relatif soit instationnaire et tournant, on fera un raisonnement simplifié considérant l’écoulement relatif stationnaire et uniforme.
La Figure 7 présente une coupe de turbine à flux transverse par un plan perpendiculaire à l’axe de rotation. (turbines de la Figure 3 b) ou de la Figure 9). L’écoulement est supposé contenu dans ce plan. Le vecteur pointillé horizontal représente la vitesse axiale locale au niveau de la section de pale (inférieure à V0). L’autre vecteur pointillé représente l’opposé de la vitesse de rotation du profil. La somme de ces vecteurs, la flèche en trait plein, représente la vitesse relative W vue par le profil. La différence avec le rotor à flux axiale est que le profil voit un écoulement relatif variable en intensité et en direction au cours de sa rotation. L’écoulement est par conséquent instationnaire dans le repère relatif. Le vecteur plus épais représente l’effort subi par la section de pale. Bien que l’écoulement relatif soit instationnaire et tournant, on fera un raisonnement simplifié considérant l’écoulement relatif stationnaire et uniforme.
Dans ce cadre, si l’on suppose aussi qu’il n’y a pas de trainée, l’effort subi par la section de pale est un effort de portance, perpendiculaire à W. Le couple sur l’arbre est donné par la projection de cet effort suivant q. On voit qu’il est maximum vers 90°-135° et 270-315° et nul vers 0° et 180° ; en considérant la trainée, ces deux positions induisent en réalité un couple négatif qui freine la turbine. L’écart type entre le couple maximum et minimum sera d’autant plus faible que le nombre de pales est grand. Il peut aussi être réduit en enroulant les pales de façon hélicoïdale le long de l’axe z. Comme l’incidence relative du fluide sur la pale change de signe entre le demi-disque amont et aval, il en est de même pour la composante radiale de l’effort subi par la section de pale. Par conséquent, la pale subi un effort de flexion dirigé vers l’intérieur dans le demi disque amont et dirigé vers l’extérieure dans le demi disque aval. Cette sollicitation alternative, se répétant à chaque cycle, constitue une cause de fatigue importante.
3. Carénages
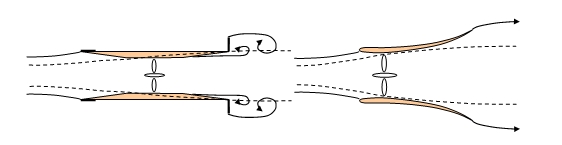
Les carénages sont des structures fixes disposées en périphérie de rotor pour en augmenter la puissance. La compacité des hydroliennes facilite l’introduction de ce type de dispositif. Les Figures 8 et 9 présentent quelques hydroliennes carénées respectivement dans le cas de turbines à flux axial et transverse.
Ces carénages créent un effet d’entonnement qui augmente le débit passant dans le rotor. La trainée exercée par le fluide sur le carénage se traduit par une dépression à la sortie de celui-ci qui est à l’origine du phénomène d’aspiration. On peut classer les carénages en deux familles se distinguant par l’origine physique de la trainée induite par l’écoulement.
- Les venturis produisent une trainée de type visqueuse[2] due à un décollement de plus ou moins prononcé situé à l’aval du carénage. Ils sont la plupart du temps constitués de segments rectilignes délimitant des portions de carénages de sections constante, convergente ou divergente. Ils sont souvent symétriques.
- Les diffuseurs produisent une trainée de type inertielle liée au phénomène de portance hydrodynamique. Les diffuseurs sont constitués de profils d’ailes (Hydroquest-Ethic), parfois distribués en cascade (DVHT) pour augmenter l’effet d’entonnement ; ils présentent toujours une asymétrie amont avale de type élargissement.
La Figure 10 présente un schéma illustrant l’effet des carénages de type venturi (gauche) et diffuseur (droite). Le trait pointillé représente le tube de courant passant dans la turbine lorsqu’il n’y a pas de carénage alors que le trait plein est le tube de courant effectivement exploité par la turbine munie de son carénage. La puissance augmentant très rapidement avec du débit passant dans le rotor, il n’est pas nécessaire d’avoir un accroissement important du tube de courant amont pour augmenter significativement la puissance délivrée. Dans les deux cas, les carénages peuvent aller jusqu’à doubler la puissance de la turbine nue.
Les carénages des turbines à flux axial de la Figure 8 sont de type venturi alors que ceux des turbines à flux transverse de la Figure 9 sont de type diffuseur. Les géométries de carénages ont été largement étudiées aux premières heures du développement de l’énergie éolienne. Les études concernant les performances des hydroliennes carénées sont moins nombreuses que celles concernant les éoliennes. Mentionnons celle menée sur le prototype à flux transverse DHVT de 2,4 m* (Figure 9 a) qui a permis d’obtenir un rendement de 60% (maximum théorique donnée par la théorie de Betz, voir ci-après) alors qu’en pratique le rendement d’une hydrolienne sans carénage se situe en général dans la gamme de 20% à 35%.
4. Limite théorique de rendement : théorie de Betz
La théorie 1D est à la base des modèles de dimensionnement utilisés pour les rotors à flux axial ou transverse. La plus connue est la théorie de Betz, qui considère le rotor comme un disque d’action créant une discontinuité de pression. L’écoulement considéré est monodimensionnel (1 tube de courant) et stationnaire; les seules pertes d’énergie de l’écoulement se situent au sein du rotor. Cette théorie ne regarde ni la forme du système plongé dans l’écoulement ni sa nature, turbine ou simple grille, pourvu qu’un saut de pression puisse lui être associé.
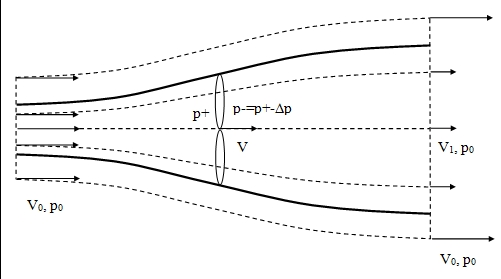
Le schéma de la Figure 11 présente les lignes de courant associées au modèle. Par commodité, le rotor schématisé est à flux axial, mais il peut être aussi à flux transverse de forme troposkienne, rectangulaire ou autre. On note V0, V et V1 les vitesses, respectivement à l’amont, dans la turbine et à l’aval. Notons qu’à l’aval, en dehors du sillage, l’écoulement récupère sa vitesse amont V0. Le tube de courant est par conséquent le siège d’une discontinuité de vitesse dans la zone avale. On note p0, p+ et p- les pressions respectivement à l’amont, devant le rotor et derrière le rotor. Le saut de pression p+-p- est noté Dp. A l’aval, la pression dans le sillage récupère la valeur de la pression à l’extérieur P0 car les lignes de courant perdent leur courbure. Enfin, le poids du fluide peut être intégré dans le terme de pression en utilisant la pression modifiée p*=p+rgz. Pour simplifier l’écriture, p* est noté p. La théorie présentée s’applique donc au cas d’un axe de rotation orienté arbitrairement.
La relation de Bernoulli appliquée à l’amont et à l’aval donne
Δp=0.5ρ(V20−V21)
La force de trainée F de l’écoulement sur le rotor est donnée par :
ΔF=ΔρS=0.5ρS(V20−V21)
où S est la surface balayée par la rotor (surface du disque d’action).
Une deuxième expression de F est obtenue par le théorème des quantités de mouvement. Pour un domaine fermé, il stipule que le débit de quantité de mouvement sortant –entrant du fluide est égal aux forces extérieures appliquées au domaine. Prenons le domaine délimité par les sections amont et avale et par le tube de courant. On obtient :
Q(ρV1)−Q(ρV0)=−F
où Q désigne le débit passant dans le tube de courant. F est la perte de quantité de mouvement axiale du fluide. Notons que les efforts de pressions au contour du domaine, qui devraient apparaître au second membre, sont omis. On montre que leur contribution est nulle.
En utilisant Q=SV et en identifiant les deux expressions de la force F on obtient :
V=0.5(V0+V1)
La vitesse dans le disque du rotor est la moyenne des vitesses amont et avales. On introduit classiquement le facteur d’induction a qui est un paramètre adimensionnel représentant le ralentissement du fluide par la turbine :
V=(1−a)V0
et
V1=(1−2a)V0
En introduisant le coefficient de trainée CF, on obtient son expression en faction du facteur d’induction a :
CF=F0.5ρSV20=4a(1−a)
La puissance P étant donnée par le produit FV, on peut procéder de même pour le coefficient de puissance CP :
CP=P0.5ρSV30=4a(1−a)2
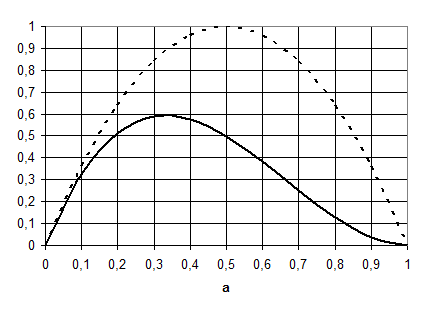
CP est aussi appelé rendement de la turbine. Il mesure la puissance P absorbée par la turbine ramenée à la puissance cinétique débitée par l’écoulement à travers la section S en l’absence de rotor. La figure 12 présente l’évolution de CF et CP en fonction du facteur d’induction a. Le coefficient de puissance maximum est obtenu pour a=1/3 et vaut 16/27≈0.59. Un rotor ne peut récupérer plus de 60% de l’énergie cinétique de l’écoulement amont. C’est la limite de Betz. Le coefficient de trainée correspondant vaut 8/9≈0.89. Pour a=0.5, le coefficient de trainée atteint la valeur maximum de 1. Au-delà de a=0.5, la trainée diminue. En réalité, la solution n’est pas physique car la vitesse V1 dans le sillage est négative. Dans la pratique, cette théorie est non valide lorsque a est supérieur à 0.4.
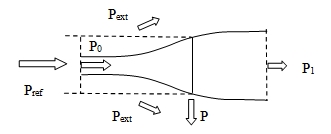
5. Limite théorique de rendement : répartition des puissances cinétiques autour de la turbine
La Figure 13 illustre la ventilation des puissances dans et à l’extérieur de la turbine. La puissance amont disponible Pref est prise comme référence. Elle se répartie en deux contributions P0 et Pext passant respectivement l’intérieur et à l’extérieur de la turbine. Une partie P de P0 est absorbée par la turbine tandis que le reste, P1, s’échappe dans le sillage. En ramenant les puissances à Pref, on peut calculer les coefficients de puissance correspondant à P0, Pext, P et P1. A l’optimum, a=1/3, on obtient respectivement:
CP0=67%, CPext=33%, CP=59% et CP1=7%
La limite de Betz de 59% s’explique essentiellement par la part de 33% qui s’échappe à l’extérieur. C’est la différence essentielle avec une turbine hydraulique de barrage qui utilise toute l’énergie amenée par la conduite. Ces dernières ont des rendements hydrauliques supérieurs à 90%. Quelque soit la turbine considérée, la théorie de Betz donne la puissance maximale perdue par le fluide dans le rotor mais ne dit pas quelle part de cette puissance est transférée sur l’arbre. En d’autres termes, elle ne donne pas accès au rendement hydrodynamique du rotor. Ce rendement est lié à la trainée que développe le profil de pale.
6. Ressource et sites d’essais
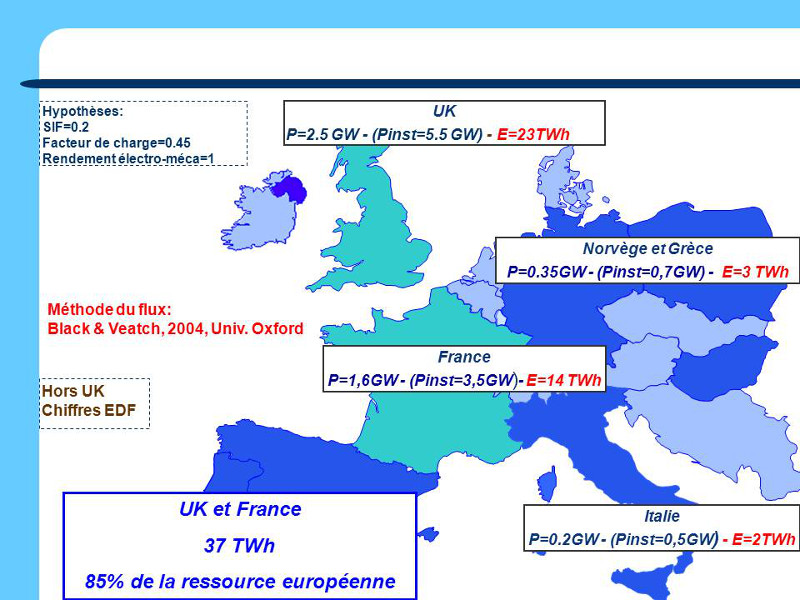
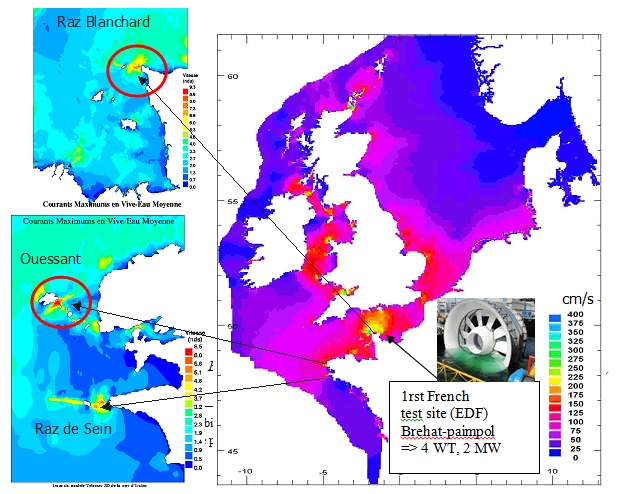
La Figure 14 représente la carte des ressources techniquement exploitables en Europe. Sur les côtes du Royaume-Uni, 106 sites intéressants ont été identifiés pour une capacité de production annuelle de 23 TWh correspondant à une capacité installée nominale de 5,5 GW avec un facteur de charge de 45%. En Bretagne, EDF a estimé l’énergie annuellement récupérable à environ 14 TWh correspondant à une capacité installée de 3,5 GW. L’addition de ces deux ressources débouche sur 37 TWh représentant 85% du potentiel européen. Ces ordres de grandeur peuvent être comparés à la production hydroélectrique en France et en Europe de 70 et 580 TWh/an. Deux conclusions découlent de ces estimations : le Royaume-Uni et la France concentrent la plus grande partie du potentiel européen ; comparé à celui de l’hydroélectricité, ce potentiel n’est pas négligeable.
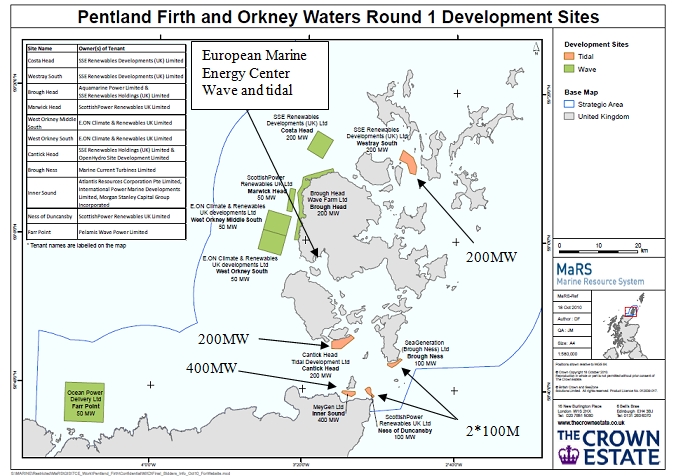
Le Royaume-Uni est à l’origine des premiers véritables tests d’exploitation de l’énergie marine sur le site d’Orkney Island, au nord de l’Écosse par le European Marine Energy Center (EMEC). Les premiers clients de ce dernier ont été Alstom TGL, Andritz-Hydro-Hammerfest, Atlantis-Resources-Corporation, Bluewater Energy Services, Kawasaki-Heavy-Industries, Voith Hydro et Open Hydro. En 2010, le Crown Estate a alloué 5 zones de licences en vue de developer des fermes d’hydroliennes pour un objectif de production de 1 000 MW en 2020 (Figure 15).
En 2008, EDF a lancé le projet Brehat paimpol. Un premier prototype de 500 kW basé sur la turbine marine EDF-Open Hydro a été installé en 2012 en vue d’une série de tests. En 2014-2015, quatre turbines devraient être installées et couplées au réseau.
En 2013, l’Agence de l’environnement et de la maîtrise de l’énergie (ADEME) a ouvert un appel pour le développement de trois à quatre fermes marines sur deux sites : Raz Blanchard et Ouessant où les courants peuvent excéder 5 m/s. Environ 40 turbines pourraient fournir 80 MW en 2020. La figure 16 expose les courants sur les côtes de Bretagne et du Royaume-Uni ainsi que la localisation des trois sites de fermes mentionnés.
Notes et références
[1] Pour se rapprocher de la situation bidimensionnelle on néglige les composantes perpendiculaires à ce tube
[2] mettant en jeu une perte d’énergie par dissipation visqueuse des tourbillons avals
L’Encyclopédie de l’Énergie est publiée par l’Association des Encyclopédies de l’Environnement et de l’Énergie (www.a3e.fr), contractuellement liée à l’université Grenoble Alpes et à Grenoble INP, et parrainée par l’Académie des sciences.Pour citer cet article, merci de mentionner le nom de l’auteur, le titre de l’article et son URL sur le site de l’Encyclopédie de l’Énergie.Les articles de l’Encyclopédie de l’Énergie sont mis à disposition selon les termes de la licence Creative Commons Attribution – Pas d’Utilisation Commerciale – Pas de Modification 4.0 International.