Énergie thermique des mers : concept et ressources

L’existence de différences de températures stables supérieures à 20°C entre la surface de l’océan et l’eau de mer située à des profondeurs de l’ordre de 1 kilomètre permet théoriquement la production d’électricité. Ce procédé s’appuie sur le concept très général de moteur thermique, où des échanges de chaleur cycliques entre une source chaude et un puits froid s’accompagnent d’une production nette de travail mécanique (Lire : La thermodynamique : énergie et entropie). En ce qui concerne l’exploitation de l’énergie thermique des mers (ETM) ainsi définie, elle est possible en principe dans une vaste zone océanique intertropicale couvrant près de 100 millions de kilomètres carrés.

1. Concept

La possibilité d’utiliser la stratification verticale de la température de l’eau de mer des régions tropicales pour produire de l’électricité fut évoquée dès la fin du 19^ème Siècle par Jacques-Arsène d’Arsonval[1] (Figure 1). Pourtant, cette notion maintenant connue sous l’acronyme ETM (Énergie Thermique des Mers) dans les pays francophones, et OTEC (Ocean Thermal Energy Conversion) dans les pays anglophones, n’est qu’une application particulière de systèmes thermodynamiques très répandus (centrales thermiques par exemple). Pour l’ETM, la source chaude du moteur thermique provient de l’eau de mer superficielle et le puits froid de l’eau de mer profonde. Ce qui distingue ces réservoirs de chaleur de ceux d’autres procédés semblables est la faible différence ΔT entre les températures des couches d’eau de mer respectives, T₁et T₂.

1.1. Cycle fermé

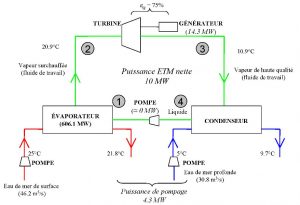
La Figure 2 illustre de manière schématique et simplifiée le fonctionnement d’une centrale ETM. Le cas choisi en toute généralité nécessite un fluide auxiliaire dit de travail qui circule selon une boucle fermée tracée en vert. Entre les Points 1 et 2, le fluide de travail se réchauffe et bout dans un évaporateur alimenté par l’eau de mer de surface. Entre les Points 2 et 3, la vapeur ainsi produite se détend dans une turbine dont le travail mécanique, converti en électricité dans un générateur, représente la puissance brute. La perte de charge subie s’accompagne d’une baisse de température. À la sortie de la turbine, le fluide de travail se liquéfie en cédant de la chaleur à l’eau de mer profonde dans un condenseur, entre les Points 3 et 4. Pour compléter le cycle, le liquide à la sortie du condenseur est pompé vers l’évaporateur (du Point 4 au Point 1).

Pour un débit de masse m donné, la description d’un cycle thermodynamique stationnaire peut se faire par un bilan d’enthalpie spécifique  h. Cette variable d’état représente l’énergie interne du fluide de travail, mais tient également compte du travail des forces de pression sur les surfaces amont et aval de tout volume de contrôle.

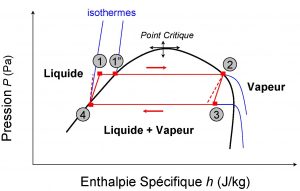
Le procédé thermodynamique qui correspond à la centrale ETM illustrée sur la Figure 2 est le cycle de Rankine. Le fluide de travail dans les deux échangeurs de chaleur évolue à pression constante (isobare). Si la turbine et la pompe étaient parfaites, les échanges de travail mécanique ne produiraient pas d’entropie[2] (une variable d’état qui caractérise la réversibilité de processus thermodynamiques). L’efficacité isentropique de machines réelles étant inférieure à 100%, une turbine produit un peu moins d’enthalpie, et une pompe en consomme un peu plus que si leur comportement était réversible. Ces points sont illustrés conceptuellement sur la Figure 3, où le parcours du fluide de travail est décrit qualitativement en termes de pressions et enthalpies spécifiques[3] (ligne rouge).

Il est intéressant de noter que pour la majorité des fluides, un changement d’état entre liquide et vapeur à pression constante se produit également à température constante[4]. La relation entre pression et température dans ce cas s’appelle la courbe de saturation[5]. Par conséquent, on peut dire que l’évolution du fluide de travail est isotherme entre les Points 1” et 2 d’une part, et 3 et 4 d’autre part. Cependant, l’ébullition et la condensation du fluide de travail dans les échangeurs de chaleur se produisent à des températures nettement différentes de celles des réservoirs thermiques correspondants; en particulier, T_evap est inférieure à T₁ et T_cond est supérieure à T₂. Cet échelonnement des températures est illustré sur la Figure 4, où la ressource thermique ΔT est non seulement allouée au fluide de travail entre T_cond et T_evap, mais permet également le refroidissement de l’eau de mer de surface dans l’évaporateur, le réchauffement de l’eau de mer profonde dans le condenseur et des échanges de chaleur dynamiques (en maintenant des écarts de température suffisants, ou pincements,  entre les fluides concernés).

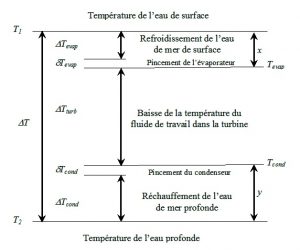La considération de cycles réversibles, ainsi que de machines isentropiques, permet souvent la dérivation de résultats fondamentaux susceptibles de corrections ultérieures. Le cas le plus connu est le cycle réversible de Carnot (deux segments isothermes, et deux segments isentropiques), dont le rendement η_C = 1 – T₂/T₁ est un maximum théorique; dans cette formule figurent les températures absolues des réservoirs thermiques, en degrés Kelvin. Le rendement d’un moteur thermique est le rapport du travail mécanique net P_cycle produit par le fluide auxiliaire au cours du cycle, sur le flux de chaleur Q₁reçu de la source chaude. Les valeurs typiques de η_C  pour les systèmes ETM sont faibles, de l’ordre de 7 %. Malheureusement, des échanges de chaleur réversibles impliquent des écarts de températures infinitésimaux entre les fluides concernés (c’est-à-dire x et y pratiquement nuls sur la Figure 3), et seraient donc infiniment lents.  Cette situation correspondrait à une puissance nulle produite au cours du cycle (travail par unité de temps).

Une approche beaucoup plus utile est de considérer des échanges de chaleur irréversibles (en temps fini) entre le fluide de travail et les réservoirs thermiques extérieurs tout en permettant au fluide de travail un parcours interne réversible (système dit endoréversible). Dans le cas du cycle de Rankine, on peut montrer que si les températures T_cond et T_evap sont suffisamment proches, le travail mécanique net produit par le fluide de travail est égal à mL(1 – T_cond/T_evap), où L est l’enthalpie spécifique de changement phase (e.g., entre les Points 2 et 1”).

En invoquant la relation de Clapeyron (qui définit la pente de la courbe de saturation), et en considérant que le fluide de travail à l’état liquide est incompressible entre les Points 4 et 1, il est facile de montrer que le travail mécanique réversible fourni à la pompe est approximativement égal au produit de (P_cycle)_rev par le rapport de la densité du fluide de travail à l‘état de vapeur sur la densité du fluide de travail à l‘état liquide (loin du point critique). Ce rapport étant très faible, d’un ordre de grandeur inférieur à 1% pour des fluides de travail adaptés, on peut donc identifier P_cycle avec la puissance brute P_brute produite par le turbogénérateur. En d’autres termes, s’il on tient compte des imperfections d’une turbine et d’un générateur réels, représentées par une efficacité ε_tg<100%, on peut écrire :

P_brute = ε_tg mL(1 – T_cond/T_evap)

En dépit de sa simplicité apparente, la formule précédente contient encore des inconnues (températures d’évaporation et de condensation), L dépend du fluide de travail alors que m est un choix opérationnel (débit massique d’une pompe). Si l’on reconnaît que pour des fluides de travail adaptés, la quantité de chaleur nécessaire pour chauffer le liquide dans l’évaporateur est nettement inférieure à L[6], on peut substituer au cycle de Rankine illustré sur la Figure 2 un cycle de Carnot équivalent en négligeant le parcours énergétique entre les Points 1 et 1”. Ceci revient à remplacer mL par Q₁.

Il se trouve que l’analyse d’un cycle de Carnot endoréversible est beaucoup plus simple[7], et se prête bien à une maximisation de la puissance produite au cours du cycle[8] (c’est-à-dire, en pratique, au choix optimal de  m pour un fluide de travail particulier[9]). Un résultat d’une élégance surprenante est que le rendement maximal de ce moteur thermique endoréversible est η_E= 1 – √T₂/√T₁. Il est clair que cette valeur est inférieure à η_C. Si les températures T₁et T₂ sont suffisamment proches, comme c’est le cas pour les systèmes ETM, η_E≈ h_C /2. L’analyse détermine également x et y, ce qui conduit, en particulier, au fait que la baisse de température dans la turbine représente environ la moitié de l’écart de température disponible lorsque la puissance est maximale. P_cycle est alors proportionnelle à (√T₁ – √T₂)², ou, dans les conditions ETM, à (ΔT)²/(4T₁) ; cette dernière approximation compense par coïncidence l’erreur commise en remplaçant mL par Q₁. Le coefficient de proportionnalité dépend des débits d’eau de mer, qui affectent le transfert de chaleur, et des indices de performance des échangeurs de chaleur.

Le choix du fluide de travail est facilité si l’on se rend compte que le cycle ETM décrit sur la Figure 2 est un réfrigérateur inversé : dans ce cas, les températures des  réservoirs thermiques sont essentiellement les mêmes, mais un moteur électrique relié à un compresseur fournit le travail mécanique nécessaire pour créer et maintenir des différences de température qui n’existent pas au départ. Les réfrigérants sont donc d’excellents candidats a priori. D’une manière plus formelle, la taille et les coûts des échangeurs de chaleur dépendent du débit volumique du fluide de travail à l’état de vapeur. Pour une valeur donnée de ce débit,  la puissance brute varie donc comme le produit de L par la densité de la vapeur. La relation de Clapeyron suggère par conséquent que les fluides dont la courbe de saturation (pression en fonction de la température) a une pente raide dans l’intervalle de température considéré sont de bons choix potentiels (Figure 5). Ce critère thermodynamique semi-empirique favorise l’ammoniac, dont les caractéristiques de transfert de chaleur sont par ailleurs très favorables.

1.2. Cycle ouvert

Conçu et breveté en France (1926) et aux États-Unis (1932)[10] par Georges Claude et Paul Boucherot, le cycle ETM ouvert utilise de la vapeur d’eau continuellement produite par ébullition partielle d’environ 0.5% de l’eau de mer de surface. À cette fin, il est nécessaire de maintenir un vide partiel de l’ordre de 3 kPa dans l’évaporateur désormais réduit à une simple enceinte. Le cycle est ouvert dans la mesure où le fluide de travail n’est pas recyclé par une pompe entre les Points 4 et 1 de la Figure 1, mais disparaît lorsque la vapeur d’eau à la sortie de la turbine se mélange à l’eau de mer froide (condenseur à contact direct) ou est évacuée après sa condensation (production auxiliaire d’eau douce).

Il est intéressant de noter que ce cycle, situé entre les Points 1” et 4 sur la Figure 3, se comporte comme un cycle de Carnot puisque le réchauffement d’un fluide de travail pompé vers l’évaporateur, entre les Points 1 et 1”, ne se produit pas. Il serait donc tentant de conclure que le cycle ouvert est légèrement supérieur d’un point de vue thermodynamique, mais le maintien de vides partiels de 1 à 3 kPa impose une consommation de puissance supplémentaire. En effet, il est nécessaire d’évacuer de manière continue les gaz non condensables (azote, oxygène) libérés de l’eau de mer sujette à de telles basses pressions[11]. En fin de compte, les bilans énergétiques nets des cycles ETM ouvert et fermé sont sensiblement équivalents.

Outre l’élégance conceptuelle du cycle ouvert, son choix dépendrait de nombreux facteurs. On peut citer comme avantages une architecture très simplifiée et un coût réduit des échangeurs de chaleur, l’élimination d’un réfrigérant et la possibilité de désalinisation. Les désavantages possibles comprennent des équipements de taille supérieure, y compris et surtout la turbine, et le besoin d’une pompe à vide. Il est certain que ces critères seraient évalués non seulement des points de vue technique et économique, mais aussi environnemental.

1.3. Bilan énergétique complet

La discussion de cycles ETM s’est limitée jusqu’à présent à la production de puissance brute dans un cycle thermodynamique tels que le cycle de Rankine illustré sur les Figures 2 (boucle verte) et 3. Or, le pompage des eaux de mer dans les échangeurs de chaleur, de leurs prises jusqu’au(x) point(s) de rejet, contribue à une consommation de puissance importante typiquement de l’ordre de 30% de P_brute. Cette fraction élevée par rapport à des centrales thermiques classiques est un résultat majeur des faibles écarts de température caractéristiques de l’ETM. Pour chaque mégawatt (MW) net, ceux-ci nécessitent des échangeurs de chaleur de plusieurs milliers de mètres carrés[12] et des débits d’eau de mer d’environ 3 mètres cubes par seconde pour l’eau de mer profonde, et sensiblement plus pour l’eau de mer de surface (en effet, au cours de l’optimisation de systèmes donnés, l’accessibilité supérieure de l’eau de mer de surface suggère généralement des débits de l’ordre de 50% supérieurs).

Une amélioration de cet état de choses se heurte à de nombreuses contraintes qui requièrent des choix et des compromis difficiles de la part des ingénieurs. Des échangeurs de chaleur beaucoup plus performants, par exemple, risquent de correspondre à des pertes de charge inacceptables tout en compliquant gravement leur entretien. En ce qui concerne la conduite d’eau froide, une réduction souhaitée de sa taille est fortement limitée par la sensibilité de la puissance de pompage au diamètre. Le terme principal à considérer est le résultat de frottements et dépend de l’inverse du diamètre élevé à la puissance 5 (pour un débit donné, une conduite 2 fois plus petite correspondrait donc à une consommation de puissance 32 fois plus grande pour couvrir ce terme). Des vitesses de pompage trop élevées, et donc des pertes de charge excessives, correspondraient aussi à un risque sévère d’écrasement de la conduite en amont de la pompe, et de cavitation. On peut noter que parmi tous les éléments énergétiques à considérer, une différence de niveau de l’ordre de 1 m due à la densité légèrement supérieure de l’eau de mer froide dans sa conduite est caractéristique de l’ETM[13]. La taille de la conduite d’eau froide, qui serait supérieure à 10 m de diamètre pour des centrales ETM de 100 MW, et sa longueur de l’ordre de 1 km la désignent même aujourd’hui comme l’élément le plus original à concevoir et le plus risqué à mettre en place.

Enfin, il faut reconnaître que la production des centrales ETM est très sensible aux changements des températures de l’eau de mer. On a déjà établi que la puissance brute dépend du carré de DT. Dans ces conditions, une variation de la ressource ETM de 1°C, par rapport à une valeur typique de 20°C, correspond à un changement relatif de la puissance brute d’environ 10%. Comme les débits d’eau de mer ne se prêtent qu’à une optimisation opérationnelle limitée, la puissance de pompage parasite n’est guère susceptible de changements importants. Il en résulte une sensibilité de la puissance ETM nette de l’ordre de 15% lorsque ΔT varie de 1°C. Il est donc important de considérer des sites potentiels d’exploitation où la ressource thermique est favorable en moyenne, mais également aussi stable que possible. Dans ces conditions, l’ETM promet d’assurer des facteurs de charge exceptionnellement élevés parmi les technologies de production d’énergie renouvelable[14].

2. Ressources

De la délimitation des régions subtropicales propices à l’exploitation de l’ETM, on passe à l’estimation des ressources ETM globales sur lesquelles pourront s’appuyer des projets de centrales.

2.1. Ressources thermiques

Il est clair qu’un rayonnement solaire intense réchauffe la surface des océans d’une manière généralement continue dans la zone intertropicale, approximativement entre les latitudes 30°S et 30°N. Des flux énergétiques compensatoires, tels l’émission d’ondes longues infrarouges, l’échange de vapeur d’eau à la surface et le transfert de chaleur sensible entre masses d’eau, atmosphère et marges continentales, permettent au système d’atteindre un équilibre. Pourtant, ceci serait bien insuffisant en soi pour expliquer la forte stratification verticale de la température des océans tropicaux. Dans le lac Tanganyika, par exemple, la diffusion verticale de chaleur a essentiellement homogénéisé la colonne liquide[15].

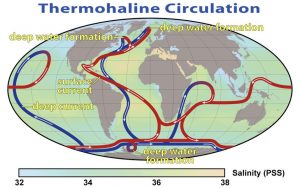
Comme le montre la Figure 7, l’existence d’eau froide profonde sous les Tropiques est le résultat d’un vaste réseau de courants planétaires qui occupe l’ensemble des grands bassins océaniques à partir de régions polaires bien particulières, où se produit une plongée d’eaux de surface plus denses. Ce grand « tapis roulant » est connu sous le nom de circulation thermo-haline (acronyme THC en anglais), car il dépend principalement de la relative densité de masses d’eau aux températures et salinités différentes. Son autre forçage vient du frottement exercé par les vents sur la surface de l’eau.

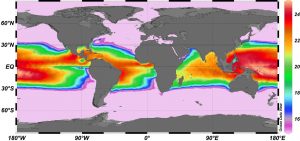
Les courants océaniques de surface, plus complexes car largement déterminés par la circulation atmosphérique et l’effet des continents (upwellings), déterminent en fin de compte quelles régions subtropicales sont vraiment propices à l’exploitation de l’ETM. La Figure 8 illustre les différences moyennes de températures entre des profondeurs de 20 m et 1000 m. On constate que les côtes occidentales des continents américain et africain sont relativement peu favorables à cause de courants froids persistants et d’upwellings. Il en est de même le long de la côte méridionale de la péninsule arabique où l’effluent de la mer Rouge a un effet prononcé. L’influence géographique de la température de l’eau profonde est généralement faible, mais se manifeste bien dans l’océan Indien par rapport au Pacifique. Enfin, il existe des bassins profonds mais relativement fermés qui ne communiquent avec les grands océans que par des seuils relativement peu profonds (mers de Sulu et Mindanao aux Philippines, par exemple); dans ce cas, la ressource thermique ETM est dégradée.

Les changements temporels des températures doivent être bien connus aussi compte tenu de la sensibilité des technologies ETM. Il est important d’éviter des régions où une moyenne annuelle acceptable cacherait des variations saisonnières trop grandes. Même s’il l’on s’attend à une grande stabilité thermique dans les océans tropicaux, il existe des zones marginales pour lesquelles la production ETM serait difficile pendant plusieurs mois, comme la côte nord du golfe du Mexique.

2.2. Ressources ETM

La connaissance des températures locales de l’eau de mer permet d’établir la puissance produite par une centrale ETM particulière. Pour de nombreux projets ETM futurs, les données disponibles, sans doute mises à jour grâce aux progrès de l’océanographie opérationnelle, seront donc suffisantes. On peut pourtant se demander quelle est le potentiel de l’ETM  à une échelle globale.

En raison du manque de réalisation pratique de cette technologie, ses partisans ont souvent eu tendance à accorder à cette question une attention limitée ou d’y répondre d’une manière opportuniste, en soulignant le caractère quasi inépuisable des ressources ETM. Pour obtenir une telle conclusion, il suffit d’invoquer le rayonnement solaire à la surface des océans tropicaux (de l’ordre de 250 W/m² en moyenne), ou peut-être l’un des flux naturels compensatoires, et de considérer la surface favorable à l’ETM (100 à 140 millions de km²). Compte tenu d’une efficacité thermodynamique nette de 1.5 à 2%, on arriverait ainsi à des prédictions de puissance électrique ETM de l’ordre de 500 TW[16], soit une trentaine de fois les besoins d’énergie primaire des sociétés d’aujourd’hui (estimés à 140 000 TWh). Cette approche n’est évidemment pas justifiée.

Alors que la ressource thermique des océans représente une différence de potentiel, comme les niveaux différents d’une centrale hydroélectrique, l’existence d’un débit de référence analogue à celui d’une rivière, est moins claire. Si on se place du point de vue d’un développement durable, il est naturel de considérer que l’eau de mer profonde se renouvelle grâce à la circulation thermo-haline. Reconnaissant ce point et estimant le débit de la THC à 30 Sv[17], Jacques-Yves Cousteau et Henri Jacquier[18] conclurent que les ressources ETM globales seraient de l’ordre de 10 TW.

Un effort a été entrepris au cours des dernières années pour examiner la possibilité d’interférences entre de nombreuses centrales ETM et la ressource thermique dont elles dépendent. Des études préliminaires simples où l’océan tropical stratifié est réduit à une seule dimension verticale, et la THC à un upwelling ambiant très lent, indiquèrent en effet l’existence d’une production ETM globale maximale limitée par l’évolution de la ressource thermique soumise à des débits d’eau de mer ETM croissants[19]. De tels modèles sont bien sûr incapables de représenter les océans dans leur complexité. Ils ignorent en particulier le fait que les phénomènes de transport (courants, turbulence) horizontaux dominent les échanges verticaux, en raison même de la stratification de la colonne liquide.

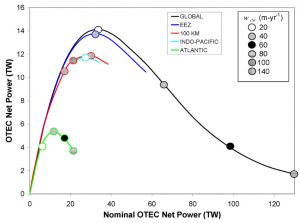
Des simulations numériques beaucoup plus intenses furent récemment complétées grâce à la disponibilité de modèles de la circulation océanique générale[20]. Ces outils sophistiqués permettent une évaluation plus crédible des interactions possibles entre un très grand nombre de centrales ETM et l’océan. Les résultats à ce jour suggèrent une production ETM maximale de 14 TW, qui correspond à une dégradation de l’ordre de 50% (rapport de l’ordonnée sur l’abscisse de la Figure 9). En revanche, des niveaux de puissance nette inférieurs à 7 TW semblent préserver la stratification thermique. Le fait que des zones d’implémentation ETM très différentes produisent des effets semblables démontre une forte télé-connexion entre des régions océaniques éloignées (le scénario GLOBAL, par exemple, couvre une surface environ 2 fois plus étendue que EEZ).

En dépit des progrès récents, de nombreux éléments de la modélisation retenue sont susceptibles d’améliorations importantes, avec, en particulier, le couplage entre l’océan et l’atmosphère. En attendant de meilleurs estimations, au vu des connaissances actuelles, il est raisonnable de penser que les ressources ETM globales sont comparables aux  besoins d’énergie primaire des sociétés d’aujourd’hui (Lire : Prospective énergétique : scénarios ANCRE).